

"Demiregular tessellation." Weisstein, Eric W, ed. This is a clear reflection that these coatings continue to evolve, crossing the borders of reality. It is about creating textures to simulate the tessellation of the different scenarios that appear in the simulator. Example 12: tessellation in video gamesĪlso known as tesellation, it is one of the most popular novelties in video games.
The tessellation of palaces such as that of the Alhambra was made up of tiles made up of ceramic pieces of many colors, with multiple (if not infinite) shapes that unleashed in geometric patterns. The tessellation during some parts of Andalusia and North Africa are characterized by geometry and epigraphy, in addition to ornamental elements such as vegetation. Figure 12 shows the tessellation of Cairo. Its name comes from the fact that this tessellation is found in the pavement of some of the streets of Cairo in Egypt. It is a very interesting tessellation, composed of pentagons with sides of equal length but with unequal angles, two of which are straight and the other three have 120º each. Non-regular hexagons with central symmetry tessellate a flat surface, as shown in the following figure: Example 10: tessellation of Cairo The parallelogram tiles a flat surface, but unless it is a square it cannot form a regular tessellation.

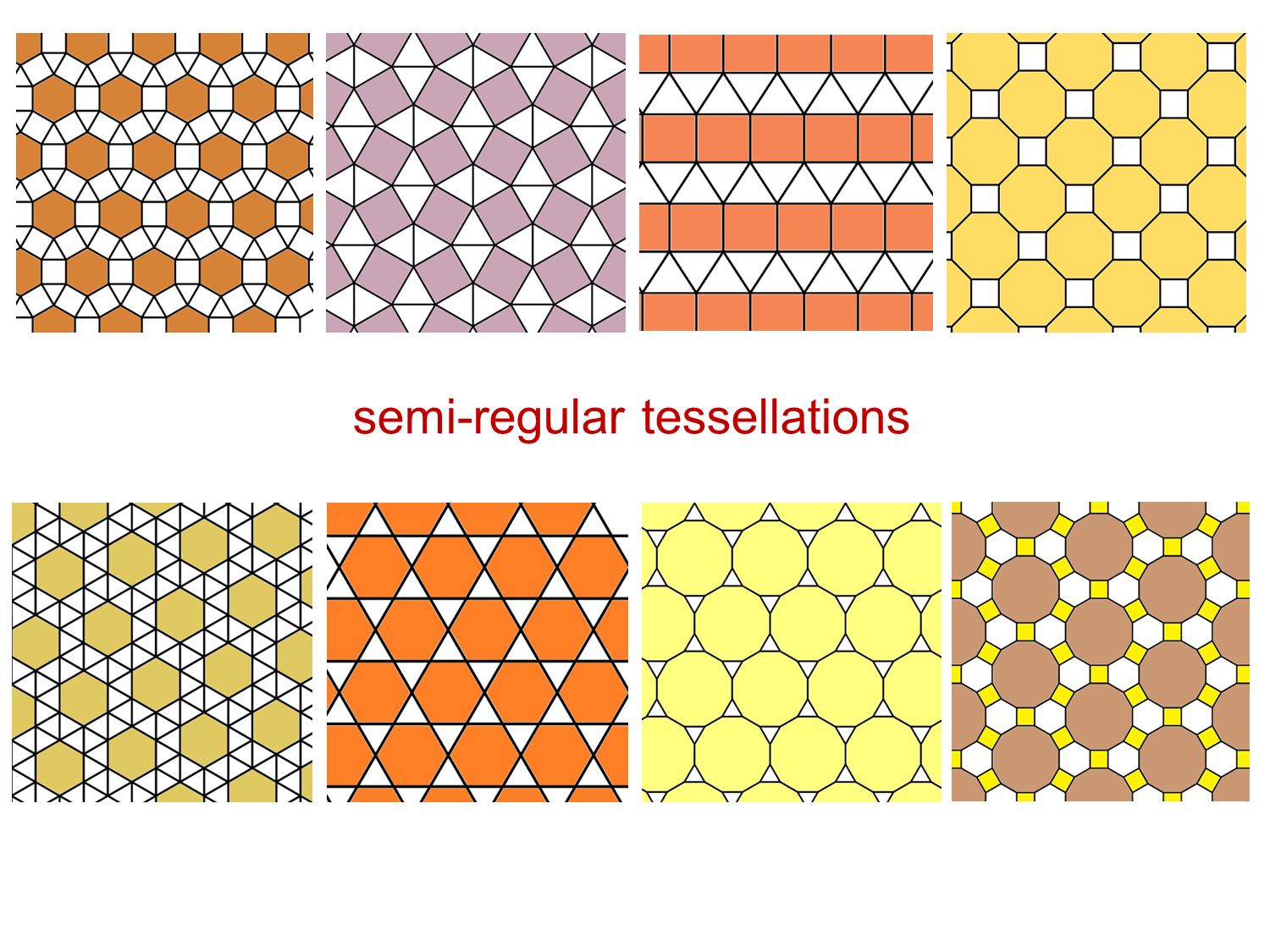
It is irregular because a node is not a common vertex of at least three squares and there are also neighboring squares that do not completely share an edge. Example 7įigure 9 shows an example of irregular tessellation, in which all the polygons are regular and congruent. Irregular tessellations are those that are formed by irregular polygons, or by regular polygons but that do not meet the criterion that a node is a vertex of at least three polygons. It is a tessellation consisting of triangles, squares and hexagons, in the configuration 3.4.6.4, which is shown in figure 8. Example 6: rhombi-tri-hexagonal tessellation Figure 7 clearly illustrates this type of tessellation. Like the tessellation in the previous example, this one also consists of triangles and hexagons, but their distribution around a node is 3.3.3.3.6. It is the one that is composed of equilateral triangles and regular hexagons in the 3.6.3.6 structure, which means that a node of the tessellation is surrounded (until completing one turn) by a triangle, a hexagon, a triangle and a hexagon. Some examples of semi-regular tessellations are shown below. 4.6.12 (truncated tri-hexagonal tessellation).3.12.12 (truncated hexagonal tessellation).3.4.6.4 (rhombi-tri-hexagonal tessellation).3.3.3.4.4 (elongated triangular tessellation).3.3.3.3.6 (blunt hexagonal tessellation).There are eight semi-regular tessellations: Each node is surrounded by the types of polygons that make up the tessellation, always in the same order, and the edge condition is completely shared with the neighbor. Semi-regular or Archimedean tessellations consist of two or more types of regular polygons.
The nomenclature for a regular hexagonal tessellation is 6.6.6 or alternatively 6 3. In a hexagonal tessellation each node is surrounded by three regular hexagons as shown in figure 5. The notation that is applied to this type of square tessellation is: 4.4.4.4 or alternatively 4 4 Example 3: Hexagonal tessellation It should be noted that each node in the tessellation is surrounded by four congruent squares. In figure 1 we have a good example.įigure 4 shows a regular tessellation composed only of squares. The most common type of tessellation is that formed by rectangular and particularly square mosaics. In the case that a single type of mosaic formed by a regular polygon is used, then a regular tessellation, but if two or more types of regular polygons are used then it is a semi-regular tessellation.įinally, when the polygons that form the tessellation are not regular, then it is a irregular tessellation. In this way, there are no spaces left uncovered and the tiles or mosaics do not overlap. Tiles or tiles are flat pieces, generally polygons with congruent or isometric copies, which are placed following a regular pattern. They are everywhere: in streets and buildings of all kinds. The tessellated are surfaces covered by one or more figures called tiles. Example 12: tessellation in video games.Example 6: rhombi-tri-hexagonal tessellation.Example 5: Blunt hexagonal tessellation.Video: 12.1 Tessellations of Regular and Irregular Polygons Content


 0 kommentar(er)
0 kommentar(er)
